Encaminarse hacia la manufactura avanzada es una oportunidad de construir, a la vez, unn futuro sólido que nace de haber cuestionado y reorientado muchas asunciones del pasado. Es, por lo tanto, importante objetivar y diseñar sus conceptos estratégicos fundamentales guiados por unos números que no son tan obvios ni comunes como los ROI, Margen o Rotación.
No son una legión de fórmulas extrañas -que de empíricas no tienen nada, pero cuya demostración obviaremos por no sernos útil ahora-, sino unas pocas. Y con algunos de sus 
criterios centrados en la obtención de flujos ágiles de un producto que, además de su supuesto e imprescindible valor añadido tecnológico, tiene unas tolerancias muy estrechas que le confieren una fiabilidad de uso extrema.
1) Comenzando por el producto, y estableciendo una relación estratégica deseable entre el rango de tolerancias y la fiabilidad, nos encontramos con que el cociente (de la distribución de Gauss):
me da un valor que, cada vez más, necesita aproximarse a 6. Y entonces, decimos que fabricamos con
“6Sigma”.
Vemos en la fórmula de K, que si estrecho las tolerancias para fiabilizar el producto, y la desviación típica
o repetibilidad () del proceso no disminuye, K bajará, y para evitarlo la única manera valida es reducir
drásticamente .
¿Por qué esto es importante a la hora de definir la estrategia de manufactura avanzada o FF?… Por una
sola razón: condiciona la naturaleza tecnológica de las máquinas y el diseño simple y robusto los procesos,
y esto afecta directamente a:
– Materiales,
– Lay outs y flujos,
– Lead times,
– Modelos de organización, e
– Inversiones
Por lo tanto, fijar esto, aparentemente tan desconectado de la concepción
de nuestra fábrica avanzada, se ha convertido en la piedra angular del proceso.
Hay más matemáticas relacionadas aquí con la propia distribución de Gauss (la “Normal”), con el SPC (control estadístico del proceso), y con la ley de fiabilidad de Weibull, pero lo básico es la fórmula (*), que debemos investigar a lo largo de los productos – procesos más críticos para conseguir el objetivo.
2) En la concepción de flujos ágiles hay más elementos, y más diversos.
a. El primero de ellos se parece al que acabamos de ver, sustituyendo la tolerancia en dimensiones/ propiedades de los productos, por rangos en los plazos de servicio.
El paralelismo es total; menos tolerancias de producto, y menos tolerancia de desviación de un plazo, ya de por sí muy corto y reduciéndose en el entorno actual y el que vendrá.
Es interesante observar lo siguiente. Si suponemos que quiero aumentar mi K (a mayor K, mayor fiabilidad de servicio también) pasando de K1 a K2, y tengo una agilidad representada por Leadtimes (LT’s), o por tiempos medios de cambio de procesos-máquinas inter-productos (T’s), es fácil demostrar que:
El efecto en agilidad necesaria es enorme: si quiero pasar de K1 = 2, a K2 = 6 (nada rara esta situación hoy en día), me encuentro con que los lead times debo reducirlos en 9 veces (tomemos 10) y los tiempos medios de set-up en 81 (digamos 100).
Y ¿en qué me condiciona esto a mi diseño estratégico de la FF?… pues, de nuevo, primero en el concepto de lay lay-out, más enfocado, inevitablemente, a trabajo en células virtuales y bajo una distribución física de un “Job-shop” con orientación a flujo (ver FIG. 1).
Las reglas SPT (shortest-processing-time) y CR (critical response) son las siguientes:
– SPT: Procesar primero en cada Workstation el trabajo que se acabe antes, completándolo.
– CR: procesar primero en cada Workstation, el trabajo que tenga un menor valor de:
Vemos su efecto, y el del concepto general del lay-out “job-shop”, en los rangos de lead-time y desviaciones obtenidos, que nos afectan de nuevo a los valores de K que veíamos antes. Aparece una interacción que requiere cálculo y prueba-error.
Notemos que el “job-shop”, bien orientado sin los errores del pasado, con tooling generalista e incremental, y servido por AGVs, da una gran versatilidad en series cortas o unitarias; tiene que ser la tendencia.
Pero la drástica reducción de tiempos inútiles no solo afecta a la distribución en planta, sino que, de nuevo, a la naturaleza de las máquinas, el diseño de procesos, materiales, modelos de organización e inversiones.
Es curioso, pues, que ambas Ks, la de servicio y la de fiabilidad tecnológica del producto, nos conduzcan a lo mismo.
b. Otra variable estratégica importante es el tamaño de los buffers de sincronización (BS) dentro de las células virtuales más intensivas. Es importante porque, si el producto es voluminoso, afectará a los espacios entre las máquinas, al lay-out y a los medios de manipulación.
Es necesario un mínimo de buffers, son un “stock” de tiempo, sincronizado, porque
no hay nada fabricándose que no tenga un flujo actual asignado hasta el
cliente o cerca de él. Su valor viene dado, en unidades, por la siguiente fórmula –derivada de la distribución de Gauss, otra vez-: BS (unidades) K · σ · LT D , donde K es la fiabilidad de “no ruptura” de la sincronización, D es la desviación típica del flujo (arrastrado por la demanda, principalmente), y LT el lead-time medio con el que responde la célula virtual.
c. La utilización de las máquinas en un “job-shop” lleva a otra discusión eterna. Un estudio puramente matemático de optimización sencilla nos da que un LT mínimo y, por tanto, un mejor servicio, se obtiene exactamente con una utilización del 50%. Pero sin duda esto no es viable, ni siquiera como media de las instalaciones pues, además, esa utilización se refiere a “sin carga” o “reserva estratégica de capacidad”. En distintas simulaciones, he obtenido un valor del 75% sin deterioro grave de dicho lead time mínimo, lo que es más razonable y realista. En este contexto, si hay que fraccionar los lotes, interesa acercarlos a un valor próximo a 1,5 T t (en unidades), donde t es el tiempo de proceso tecnológico unitario, y T el de set-up o preparación. Obsérvese que si T = t, tendíamos la utilización del 75%.
d. Hablando de lotes, la formulación más tradicional establece un valor tal que L (lote) C · T, donde C es una constante que depende de las características del proceso y producto, y T es el tiempo de cambio. No hay ninguna razón para no considerar este valor COMO REFERENCIA (otra cosa será su utilización concreta en el día a día, a veces superándolo, a veces quedándonos por debajo). Y no hay razón, porque si los T son pequeños, lo lotes también disminuirán; y mucho.
Porque, recordemos, que una adecuada –nada exagerada para la manufactura avanzada– reducción de tiempos de cambio T rondaba dejarlos en la 100ª parte; y esto supondría dividir los lotes por 10!!!
Ni qué decir tiene que el valor del lote condiciona el lay out y el diseño de los medios de manipulación, buffers, etc., así como también el modelo de organización operativa de la planta.
Existe también otro método de dimensionar lotes medios que se basa en asignar una cantidad anual de tiempo a los cambios (una cantidad estratégica, que fija indirectamente el valor de la capacidad neta disponible). Si esta cantidad es Q, y los tiempos de cambio medios son T, entonces es fácil de ver (por optimización condicionada
de Lagrange) que el lote de un producto dado, en mezcla con otros de un área o familia,
sería:
Aquí, Di es la demanda anual en unidades de un producto i, y pi su coste directo industrial.
Yo utilizaría esta segunda solamente cuando hay unas familias definidas que operan
en una célula virtual muy estable del jobshop, o si se trata de una célula real. La razón
es que, de lo contrario, no hay un criterio estratégico definible para decidir “qué
cantidad Q de inactividad por cambios asigno”, y ni tampoco un contexto de mínima
estabilidad.
O sea, que sólo es útil para lo más repetitivo, regular y de vida más larga.
e. Finalmente, tenemos el equilibrado estratégico de capacidades. Esto se expresa 
cualitativamente, en la FIG. 2. Con diversos ejemplos de tiempos de proceso generales,
el producto fluye en las máquinas del “jobshop” que cada barra representa, de derecha
a izquierda, y forma en el instante representado, una célula virtual.
Según se ve gráficamente, ocurre lo siguiente:
– En cada estrangulamiento hay una parada que aumenta el lead- time.
– La reducción del desequilibrio, por optimización de una operación más lenta “aguas abajo” (hacia la izq.), mejora el lead-time no solo en esa operación, sino en la espera, o sea, dos veces.
– La ordenación del flujo desde “máquinas más lentas a más rápidas” reduce el lead-time y lo limita al tiempo de proceso tecnológico puro, al igual que su equilibrado total.
Sobra decir que todo ello tiene un efecto en el lay-out, y aconseja también una determinada organización del flujo, y características de máquinas, procesos y modelo de organización.
Hemos visto como un conjunto de factores, aparentemente no demasiado conexos, acaban afectando al diseño estratégico de la fábrica del futuro, y que lo hacen, inva-riablemente, condicionando características de las máquinas, mate-riales, procesos, layout, tooling y sobretodo modelos de organización.
Y una vez realizado el análisis numérico de producto (punto 1) y flujos (punto 2), nos encontramos con una serie “trade-offs” que requerirán, sin duda, de un criterio de optimización. Y de nuevo, debemos objetivizar estos puntos con matemáticas. Son recomendables dos herramientas sencillas:
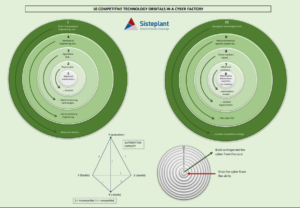
A) La investigación operativa (I.O.,FIG. 3), con los modelos conocidos del simplex (lineal), entera, mixta o no lineal (branch-bound), que nos servirá para establecer óptimos comparables (más de uno).
MAX Z = F(X1, X2)
Condicionada por: ≤ f1 (X1, X2), : ≤ f2 (X1, X2)… : ≤ fn (X1, X2)
B) Los árboles de decisión probabilísticos (FIG. 4), para afinar las alternativas completándolas con otros as-pectos cualitativos y de azar.
C) Los modelos dinámicos de Euler – Lagrange (aplicados en Mecánica), son muy útiles para determinar planes secuenciales de inversiones óptimas que minimicen el riesgo. Son una alternativa a los árboles probabilísticos del apartado anterior. Esto es de especial importancia en la manufactura avanzada de la FF por lainteracción dinámica entre tecnología-organización-personas y resultados. La preciosa demostración del
teorema está fuera del alcance de estas notas. Se trata de determinar la mejor curva Inversión (I) – tiempo(t), que minimice una función como el riesgo combinado tecnológico-organizativo-económico, r.
La mejor curva de inversión (que seguirá una forma parecida a la FIG. 5, si sus parámetros de riesgo están bien definidos), se obtiene de integrar la ecuación diferencial generada por la ecuación de Euler-Lagrange:
Esto nos dará la función I = I(t) de la FIG. 5
Como conclusión, sólo decir que merece la pena situarse y configurar objetivamente la realidad con este conjunto propuesto de medidas sencillas. Esto no está reñido con la visión de a dónde ir, sino que intenta viabilizarla y ordenarla, creándole un perímetro de conceptos y precauciones de diseño, y unos riesgos tecnológicos, organizativos y económicos aquilatados y a gestionar desde el principio del proyecto.
Autor:
Javier Borda Elejabarrieta, Dr. I.I., Msc. y MBA; Presidente y C.E.O. de Sisteplant. Profesor de la ETSII de Bilbao (Aula
Aeronáutica) y de la Universidad Juan Carlos I, (logística para Defensa).
[:]
