Diariamente salgo a correr y al menos en tres ocasiones, al llegar a casa, se me ha caído la llave por una alcantarilla de pluviales. ¿Fatalidad?… Pues he llegado a la conclusión de que NO! Por qué?.
1. ¿Fatalidad? ¿Casualidad?
Cuando me paro y pienso en racionalizar esta demoníaca situación me doy cuenta de varias cosas:
- Corro todos los días.
- El registro está en mi senda.
- Está enfrente de la puerta de entrada, y la llave la llevo en la mano. Como he acabado, ya estoy relajado y pensando en otra cosa, estoy en “mis dominios”, y tiendo a aflojar la palma.
- Aunque la alcantarilla tiene una superficie pequeña y sólo con un 50% de huecos (estrías), es significativa respecto al ancho del camino.
- Como al caer, la llave rebota una distancia bastante precisa, y gira y tiende a ponerse vertical, puede entrar y se cae por las rendijas de la alcantarilla.
- Etc…
Las tres veces es un ejemplo de ocurrencia reiterada de algo sumamente improbable. Pero ¿Improbable? … No tanto:
- Se dan condiciones físicas objetivas permanentes (mi ruta, la superficie, me relajo, el rebote, …)
- Hay repetición constante
- Los factores anteriores no son tan independientes como pueden parecer; por ejemplo, si me aparto de la senda, me relajo, aflojo la mano, y es más fácil que caiga. Y como la llave rebota en el suelo, acaba con bastante probabilidad en la alcantarilla.
Esto me recuerda alguna frase genial sobre la incertidumbre y la aparición de lo improbable: “un día inusual es aquel en el que no hay nada inusual” (Persi Diaconis).
O, “predecir es muy difícil, especialmente el futuro” (N. Bohr).
Lo que me lleva a pensar que tenemos que ir hacia 6-7 y más Sigma en la calidad de producción “a la primera”, por las razones que tanto he reiterado en otros artículos (ver en www.sisteplant.com: “Capacidad de fabricación con 6Sigma en la fábrica del futuro” y “Misión del mantenimiento avanzado en las operaciones de fractura hidráulica (“fracking”),) y también recomiendo el libro de D.J. Hand de Scientific American titulado: “The principle of improbabilty”.
Tenemos un problema, pero que es gestionable hasta un cierto límite. ¿Cómo lo vamos a hacer entonces?
2. Las causas de todo
Lo primero es conocer al travieso demonio de la variación; qué le gusta, de qué se alimenta y cómo actúa.
Básicamente, podemos suponer tres grupos de leyes que lo acogen:
- Leyes de la naturaleza (algunas muy sutiles y contraintuitivas)
- Leyes de la estadística (algunas también muy sutiles y poco o nada intuitivas)
- Leyes subjetivas, psicológicas, o no tanto.
Lo que consideramos “improbable” depende de la escala a la que me muevo:
- Para una persona, algo improbable es del orden de 10-6.
- En la tierra, es del orden de 10-15
- En el universo es de 10-50
Lógico, porque juega el tamaño del sistema y la cantidad consiguiente de sucesos que en él ocurren. Y que son Meganúmeros excepcionales, por la explosión combinatoria.
Veamos una a una estas leyes.
a) Leyes de la naturaleza que afectan a la frecuencia de la improbabilidad
Aunque parezca extraño, el principio de incertidumbre de Heisenberg, y la mecánica cuántica en general, generan caos, y “afectan con minúsculos y continuos cambios”, cuya combinatoria, unida a la afinidad atómica -por remota que ésta sea-, acaban dando una tendencia a que múltiples fenómenos improbables sucedan.
Pensemos, por ejemplo, en los microfallos y microparadas en el funcionamiento de las máquinas; lo que nos queda y es tan difícil de eliminar una vez que hemos resuelto los problemas asignables. La dispersión remanente inevitable de cualquier proceso industrial; NO se pueden conseguir “¥ sigmas”

Estos pequeños y continuos cambios acaban precipitando un fallo mayor, porque su combinatoria imperceptible para nosotros, hace al final mucho más probable de lo que intuimos que puedan sumarse.
Esto nos dice que el presente condiciona el futuro, pero que el “presente aproximado” no determina lo que será un “futuro aproximado”. Algo inquietante.
Otra causa física, aunque algo más accesible para su tratamiento, son las imperfecciones mecánicas, frecuentemente microscópicas.
Como si, por ejemplo, una moneda no tuviera una planitud exacta, y entonces los momentos cinéticos hacen que caiga con sesgo, dando a largo plazo más, digamos, caras que cruces.
b) Leyes probabilísticas, no tan obvias
Los modelos de probabilidad son, como tales, imperfectos. Para empezar, la probabilidad es un límite del cociente casos favorables/casos posibles cuando el número de experimentos tiende a infinito.
Pero el infinito no es materializable por nosotros, y es contraintuitivo. Y aunque no fuera así, las causas físicas que acabamos de ver, acaban alterando las leyes de los modelos estadísticos que aplicamos. Sin que lo notemos, muy poco a poco. “nunca te bañarás dos veces en el mismo río”, dijo Heráclito.
En la industria, por razones de economía, suponemos equivocadamente, en el control de calidad (a desterrar como propugnamos en el anteriormente citado artículo de 6 sigma (“Capacidad de fabricación con 6Sigma en la fábrica del futuro”), que “nuestras óptimas” son suficientes. La realidad es que, para empezar, no cumplen la ley de los grandes números, y para continuar, se ven afectadas por los factores vistos anteriormente. Entonces, las sorpresas llegan con frecuencia, y con suerte llego a un 3Sigma sostenido como resultado en el cliente, pero con un 2Sigma en la capacidad de producción interna “buena a la primera”.
Por eso, la única forma sana de actuar es buscar la repetibilidad y alta capacidad de procesos en ellos mismos, que son la fuente, y hacerlo de una forma mucho más científica.
Otro factor estadístico es la “palanca de probabilidad”, que significa que una ligera variación en las tolerancias admisibles de los procesos, o en el modelo matemático real de la distribución de frecuencias, implican sustanciales cambios en la probabilidad. En el primer caso, por la no linealidad de la curva más utilizada, la curva de Gauss, y en el segundo porque hay distribuciones estadísticas muy similares (como la exponencial pura o la de Cauchy) que dan resultados muy diferentes para la probabilidad de cada suceso (por ejemplo, el valor de una propiedad física, como medida, peso, dureza, etc.). Se puede apreciar esto en la siguiente figura.

Pero, además, frecuentemente las distribuciones no son totalmente simétricas, porque la realidad no es 100% aleatoria en los pequeños incrementos de valores alrededor de la media. Hay sesgos porque, por ejemplo, pueda ser más fácil que algo se desvíe a menos que a más debido a condiciones físicas del proceso. Esto aún apalanca más, y lo improbable, se hace probable.

Diferencia de probabilidad unitaria no simultánea
Como resultado del apalancamiento, aparecen las siguientes probabilidades para distintos eventos:

Lo que supone una diferencia abismal. Por eso, una modelización deficiente de la distribución, desviándose de la estándar de Gauss, origina que aparezca lo que pensamos es “extremadamente improbable”.
La consecuencia de todo esto es que merece la pena un esfuerzo continuado en refinar esos modelos estadísticos. Y adaptarlos a mi caso: yo tengo mis procesos y mi casuística, que no son un estándar de la industria, sino los míos, que utilizo unas máquinas, materiales, personas y prácticas de ingeniería y de producción que son propias y diferentes.
Por último está el factor de cómo medir las variables. Pongamos, por ejemplo, el conocido MTBF (tiempo medio entre fallos), que utilizamos mucho en fiabilidad de equipos y mantenimiento avanzado por RCM.
Si superamos una cadena de fallos en el tiempo, y cojo una ventana de 1 mes para medirlos.

Basándonos en la figura, si cojo, por ejemplo, una ventana de 1 mes, veo, y me alarmo, por 3 fallos concentrados “que jamás se dan”. Pero si yo hago “rodar” de forma continua esa ventana, veo que no es tan infrecuente (posición A).
Los “períodos fijos” son peligrosos porque alteran los análisis y hacen que se diseñen modelos probabilísticos imperfectos que originan el apalancamiento de error que hemos visto antes.
Recomiendo, por todo, utilizar con cuidado las pruebas de hipótesis y normalidad de las distribuciones con la (Ji)2 u otras herramientas, y apoyarse en el teorema de Bayes para comprobarlas.

c) Finamente, veamos las Leyes subjetivas.
Tienen dos aspectos:
- En el primero, la mente altera la interpretación de resultados porque, al parecerle improbables en extremo, piensa, por ejemplo, que simplemente ha habido errores en la medida.
Solo para evitar esto, y que se lleven a cabo acciones erróneas sobre los procesos, tiene sentido lo que en este artículo propugno.
- En el segundo, pienso en que es probable que ocurra algo, por remoto que sea y, sin darme cuenta, aplico pequeñas acciones inconscientes día a día que acaban precipitándolo.
Ningún problema hay sí “lo que pienso es positivo”, pero todos si es “negativo”, y precipito el fallo catastrófico. En este caso, la solución es también modelizar con precisión.
3. Ayuda por software inteligente
Hemos introducido cómo la modelización precisa de los fenómenos es importante si quiero llegar a tener una robustez extrema en las propiedades y fiabilidad a largo plazo de productos y procesos.
La modelización precisa no es tarea fácil, y requiere tanto un buen nivel de ingeniería, como ayudas de software inteligente y amigable.
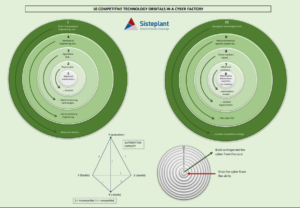
Para ello, en Sisteplant hemos desarrollado y lanzado Promind, que contiene modelos de análisis estadísticodinámico y profundo, simulación, pruebas inteligentes de hipótesis y, especialmente, modelización precisa de los fenómenos físicos que están detrás del fallo y sus probabilidades. La FIG. 4 muestra su concepto genérico.

4. Conclusión
La profundización en lograr capacidades de proceso “a la primera”, más allá del 6Sigma, es necesaria para competir en el futuro, fabricando tolerancias muy estrechas con repetibilidad, y ofertando productos fiables a largo plazo y con calidad 100%. Pero esto requiere planteamientos científicos y modelización precisa de los fenómenos detrás de la variación y de los fallos. Lo contrario arrastra al fatal empirismo del “prueba-error”, y de ahí a la “magia-brujería” hay solo un paso. El empirismo es necesario, claro, pero sin el esfuerzo paralelo de modelización es una ruina para progresar tecnológicamente.
Hemos visto en este artículo los factores que determinan las imprecisiones que nos impiden recorrer el camino, y cómo eliminarlos para poder utilizar con éxito una ayuda de software inteligente, al final necesaria absolutamente para afinar a esos extremos.
Autor:
Javier Borda Elejabarrieta, Dr. I.I., Msc. y MBA; Presidente y C.E.O. de Sisteplant. Profesor de la ETSII de Bilbao (Aula Aeronáutica) y de la Universidad Juan Carlos I, (logística para Defensa).
[:]